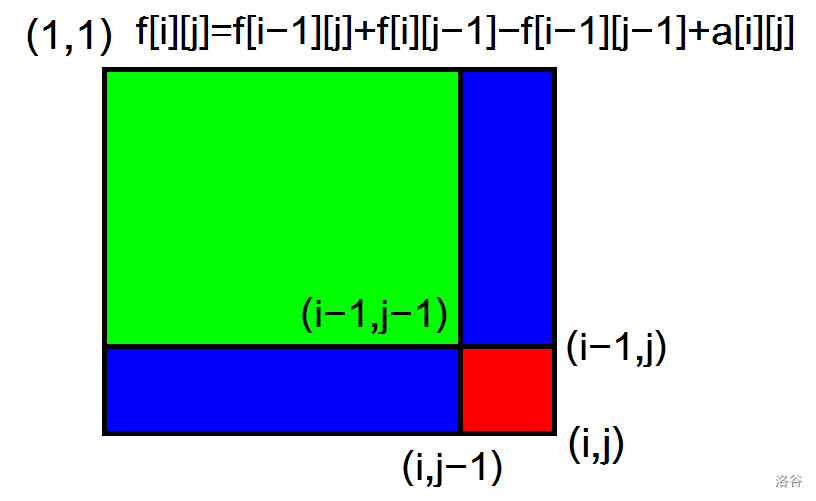ETT(Euler Tour Tree)学习笔记
-1. 导入
当维护一个动态变化的树时,最常用的数据结构就是 Link-Cut Tree 了,但是有的毒瘤出题人总是出一些这样的阴间问题:
把以 x 连带它的子树整个接在节点 y 的下面。
把以 x 为根的子树权值都加上 y 。
常规的LCT无法解决这样的问题,怎么办?
肯定有大佬会跳出来说:我会LCT维护虚子树信息!
然而这样简单的LCT就会细节巨多,稍微写错一点就会全部木大。我们需要一种更加适合我这种蒟蒻、更简单的数据结构—— ETT 。
Notice :真正的ETT能够实现更加复杂的功能,然而写起来也更加困难,写题时经常使用的是使用牺牲了一部分功能的简化版,即伪ETT。本文主要介绍的也是伪 ETT 。
0. 目录
什么是 ETT ?
ETT 怎么写 ?
2.1. 前置芝士 : 括号序。
2.2. 前置芝士 : 伸展树。
2.3. 操作 1. 把以 x 连带它的子树整个接在节点 y 的下面。
2.4. 操作 2. 查询从 x 到根的和。
2.5. 操作 3. 连接/断开一条从 x 到 y 的路径。
2.6. 操作 4. 给一个以 x 为根的子树内所以节点权值集体加 k 。
2.7. 关于时间复杂度。
思考题。
例题: P4219 。
思考题答案。
1. 什么是 ETT ?
在学习一种数据结构之前,我们要先弄懂这个数据结构要实现什么功能。
ETT 是维护动态树的数据结构,主要支持如下功能:
把以 x 连带它的子树整个接在节点 y 的下面。
把以 x 为根的子树权值都加上 y 。
查询从 x 到根的信息(如求和)。
连接一条从 x 到 y 的路径,保证原先 x 和 y 不连通。
断开一条从 x 到 y 的路径,保证原先 x 和 y 直接连通。
……
ETT 比 LCT 支持更多操作,但是常数比 LCT 大得多。故如果不需要维护、修改子树信息,还是老老实实写 LCT 吧。
2. ETT 怎么写?
2.1. 前置芝士:括号序(出栈入栈序)
话说欧拉环游树为什不用欧拉序反而用括号序。<-因为是伪 ETT 啊。
" DFS 进入某个节点的时候记录一个左括号 ( ,退出某个节点的啥时候记录一个右括号 ) 。每个节点会出现两次。相邻两个节点的深度相差 1。"(来自 OI-wiki )
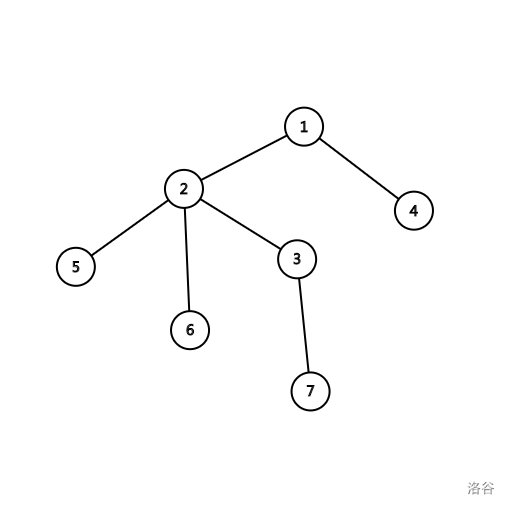
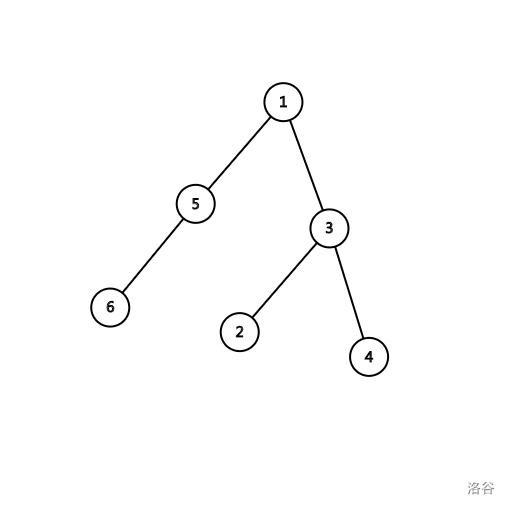
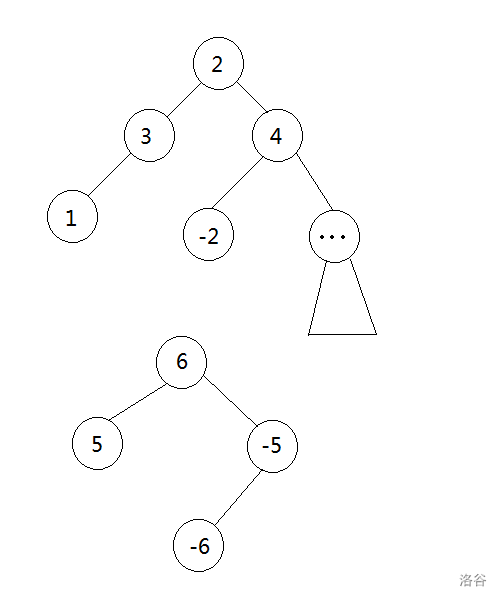
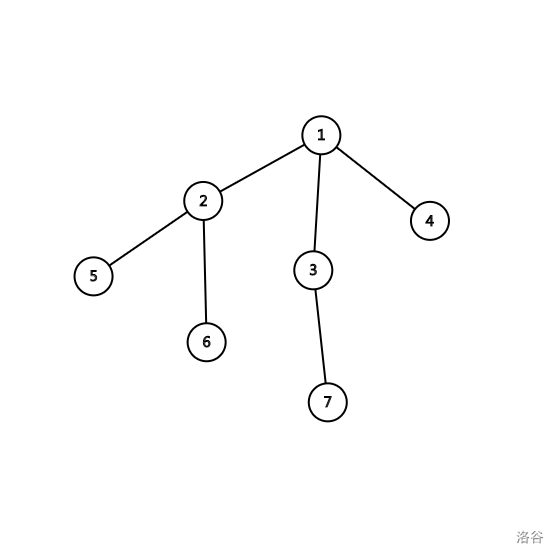
比如这样一棵树:
它的括号序长这样(这里记下了节点编号,以入栈为正,出栈为负,而不是单单记录左右括号):
1 2 5 -5 6 -6 -2 3 7 -7 -3 4 -4 -1
如果点上带权值呢?
简单转化一下,入栈时记录该节点的正权值,出栈时记录该节点的负权值。(下面将这种方式得到的括号序列简称权值括号序列)。
2.2. 前置芝士:伸展树( splay )
东西较多,很短的篇幅讲的也不能很细,就丢一篇过往的洛谷日报了
洛谷日报62.Splay简易教程
学会了括号序和splay,就珂以正式学习ETT啦
2.3. 操作 1. 把以 xx 连带它的子树整个接在节点 yy 的下面。
我们先来看看ETT最独特的操作。
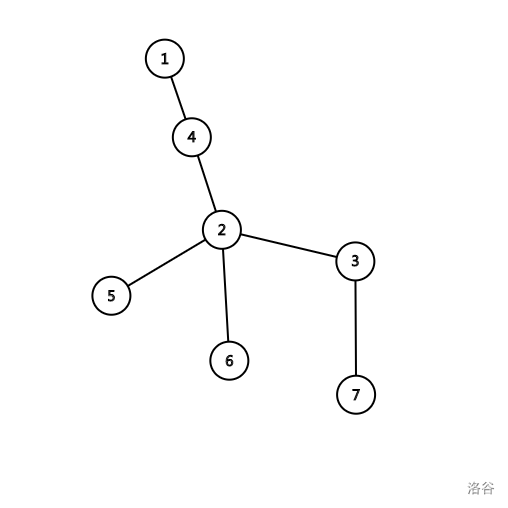
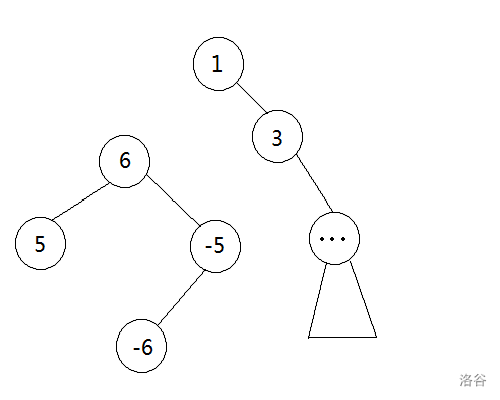
还是上面那张图,我们把3号节点接到2号下面试试。
好像没什么特别的,我们再写下它的括号序试试:
现在的序列是: 1 2 5 -5 6 -6 3 7 -7 -3 -2 4 -4 -1
先前的序列是: 1 2 5 -5 6 -6 -2 3 7 -7 -3 4 -4 -1
发现了什么?好像直接把 3 7 -7 -3 平移到了 -2 前面就行了?
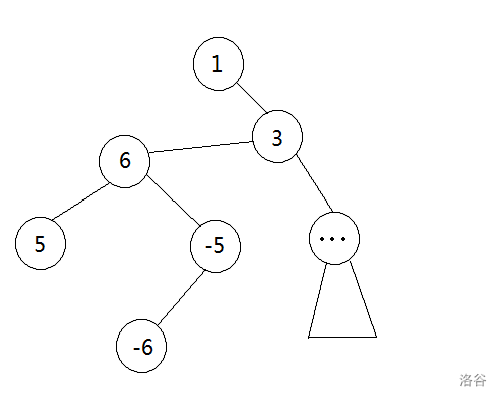
别慌,再来试一下,这次我们把2号节点接到4号下面。
再次写下它的括号序列:
现在的序列是: 1 4 2 5 -5 6 -6 3 7 -7 -3 -2 -4 -1
先前的序列是: 1 2 5 -5 6 -6 3 7 -7 -3 -2 4 -4 -1
这次把 2 5 -5 6 -6 3 7 -7 -3 -2 平移到了 -4 的前面。
看来真的只是平移就行了。
可以这样理解:一个节点 x 的入点和出点之间维护了一整个以 x 为根的子树信息,把这一段区间平移就相当于把整个以 x 为根的子树平移。
总结一下:把 x 节点接到 y 节点下面只需要一步:把从 x 的入点到 x 出点这一整段平移到 y 出点前,或者 y 的入点后。
2.4. 操作2. 查询从 x 到根的和。
只需要记录权值括号序列到这个节点的入点的前缀和就行了。读者可以自证不难
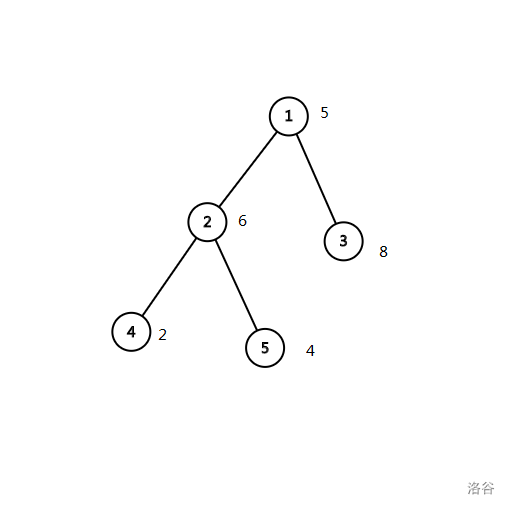
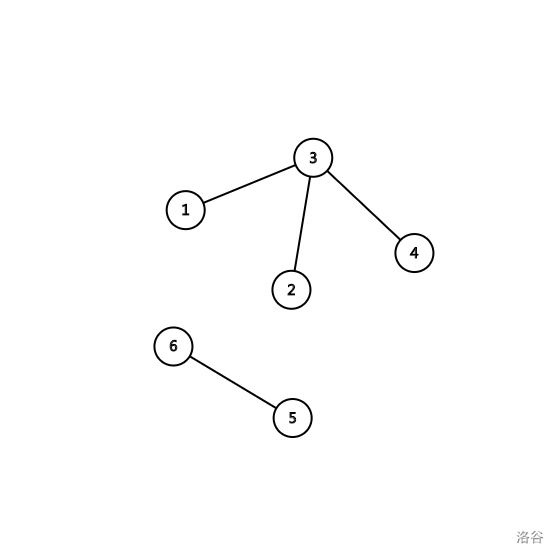
以下面这张图为例:
它的权值括号序列为:5 6 2 -2 4 -4 -6 8 -8 -5
查询从1到5的权值和,我们发现恰好是从第1个数到第5个数的和。
可以再感性理解一下,如果一个节点 y 不在从根到查询的节点 x 的路径上,要么在x的入点之前,与自己的出点相抵消,要么不在这段前缀和内。(如果还是觉得难以理解可以先深入地学习一下括号序)。
好了,你已经学会了ETT了
现在问题就转化为了怎么平移一段区间。
让我们隆重请出序列之神—— splay 。
( splay 区间平移也有多种方法,这里只讲我自认为比较简单的一种。)
众所周知, splay 可以翻转区间(不会的可以看看模板题),我们来看看怎么把这个功能用起来。
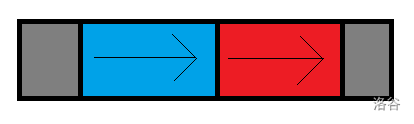
这是原序列,我们想把红色的部分移到蓝色的部分前面。
我们先把红蓝两部分一起翻转。
红色部分就跑到蓝色前面去了。可惜是前后翻转的,我们把这两部分分别翻转过来。
区间平移就完成啦。
2.5. 操作 3. 连接/断开一条从 x 到 y 的路径。
Notice : 有大佬指出这种方法只是换父亲,并不是真正的 link-cut ,因为本文主要介绍的是伪 ETT ,有想学习真正的 ETT 的读者可以自行学习。
先看连边的情况。
这个好像有点复杂,因为,从树上平移跑到森林里去了。
我们再请出一张图:
可以得到两个括号序:
1 3 2 -2 4 -4 -3 -1
5 6 -6 -5
现在我们把5号节点接在1号后面。
新的括号序只有一个括号序了:
1 5 6 -6 -5 3 2 -2 4 -4 -3 -1
我们发现,这就是直接把第二个括号序列强塞在了1的后面。
反过来,当我们切断5号和1号之间的边时,就是直接把 5 6 -6 -5 单独分裂出来。
继续考虑用splay森林来维护这一堆括号序列
对于同一棵树上的修改,直接像刚才一样翻转就好。
当连接两个节点时,把深度较大的节点所在的 splay 合并到较浅的节点的 splay 中。
更具体地:使用上面的例子。
这是合并前的 splay :
我们把1提到根,再把第二个数(3)提到1的右子树。
3的左子树就空出来啦,我们可以直接把这个 splay 接到这里,就完成了区间合并的操作。
更一般的,我们的操作分三步:
找到插入位置前一个数,把它提到所在 splay 的根。
找到插入位置后一个数,把它提到所在 splay 的根的右儿子。
这时所在 splay 的根的右儿子的左儿子一定是空的,我们可以直接把要插入的 splay 接在这里,别忘了及时更新信息。
断开时同理,也分三步。
找到断开区间的前驱,把它提到所在 splay 的根。
找到断开区间的后继,把它提到所在 splay 的根的右儿子。
这时所在 splay 的根的右儿子的左子树一定代表整个要断开的区间,我们可以直接把这里断开,当然也要及时更新信息。
Notice:这里讲到的方法是不支持换根的,如果要支持换根和动态连接和断开,可以进行一个ETT的看。
2.6. 操作 4. 给一个以 xx 为根的子树内所以节点权值集体加 kk 。
简单,只要给 x 的入点加 k ,给 x 的出点减 k 。那么只有这个子树内的节点会受到影响加了 kk 。
2.7. 关于时间复杂度。
因为都是 splay 维护的序列上的问题,单次修改和查询的时间复杂度当然也是 O(logn)O(logn) 啦。
3. 思考题
你真的学会了 ETT ……吗?这里有几道思考题,答案在代码后面,读者可以思考思考,检测一下自己有没有真正理解 ETT 。
如果答对了,那么你真的学会了 ETT ,快去写道模板题练练手吧。
ETT 可以实现 findroot 操作吗?如果可以,如何实现?如果不能,理由是什么?
为什么断开区间的前驱和后继一定存在?(保证数据合法)
如何计算以一个节点 x 为根的子树大小?
能不能用 ETT 维护路径和一样维护路径最大值?
相关题目:
[BZOJ3786] 星系探索(模板题)
P4219 [ BJOI2014 ] 大融合
4. 例题
P4219 [BJOI2014]大融合
题目大意:
给你 n 个点,支持动态连边,查询一条边左右两边子树大小的乘积。保证数据合法。
思路:
子树问题用 ETT 一般能简化许多,我们试试在这里使用 ETT 。
给的图是个森林,先给每个树指定一个根,把深度处理出来。
连边时按 ETT 的方法正常连即可。至于维护子树大小,写在思考题里了,没想出来可以看一下答案。
对于每个询问,我们求出深度较深的那个子树大小 Siz ,用整颗树的大小减去 Siz 就是这条边连接的另一棵子树的大小,相乘就是答案。
代码:
1 |
|
本人马蜂比较清奇且常数巨大,不喜轻喷。
另外这份代码只是通过了 P4219 ,不保证完全正确,如果您发现锅了欢迎来打我的脸。
5. 思考题答案
可以,找到整颗 splay 的最靠左的节点(括号序列的第一个值)。
因为这段区间一定包含在它爸爸的入点和出点之间,不可能在整段序列的头部或尾部。
类似删除:再分三步:
找到 x 的入点的前驱,把它提到所在 splay 的根。
找到 x 的出点的后继,把它提到所在 splay 的根的右儿子。
同样这时所在 splay 的根的右儿子的左子树(为了方便叙述,记为子树 Y )一定代表整个以 x 为根的子树的括号序列,又因为这段括号序列同时包括这颗子树内所有点的出点和入点(每个点两次),我们直接将子树 Y 的大小除以二作为答案。
不行,因为最大值不具有区间可加性,不能保证求到的答案在这条路径上。(这并不代表 ETT 不能维护链最大值)。